💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
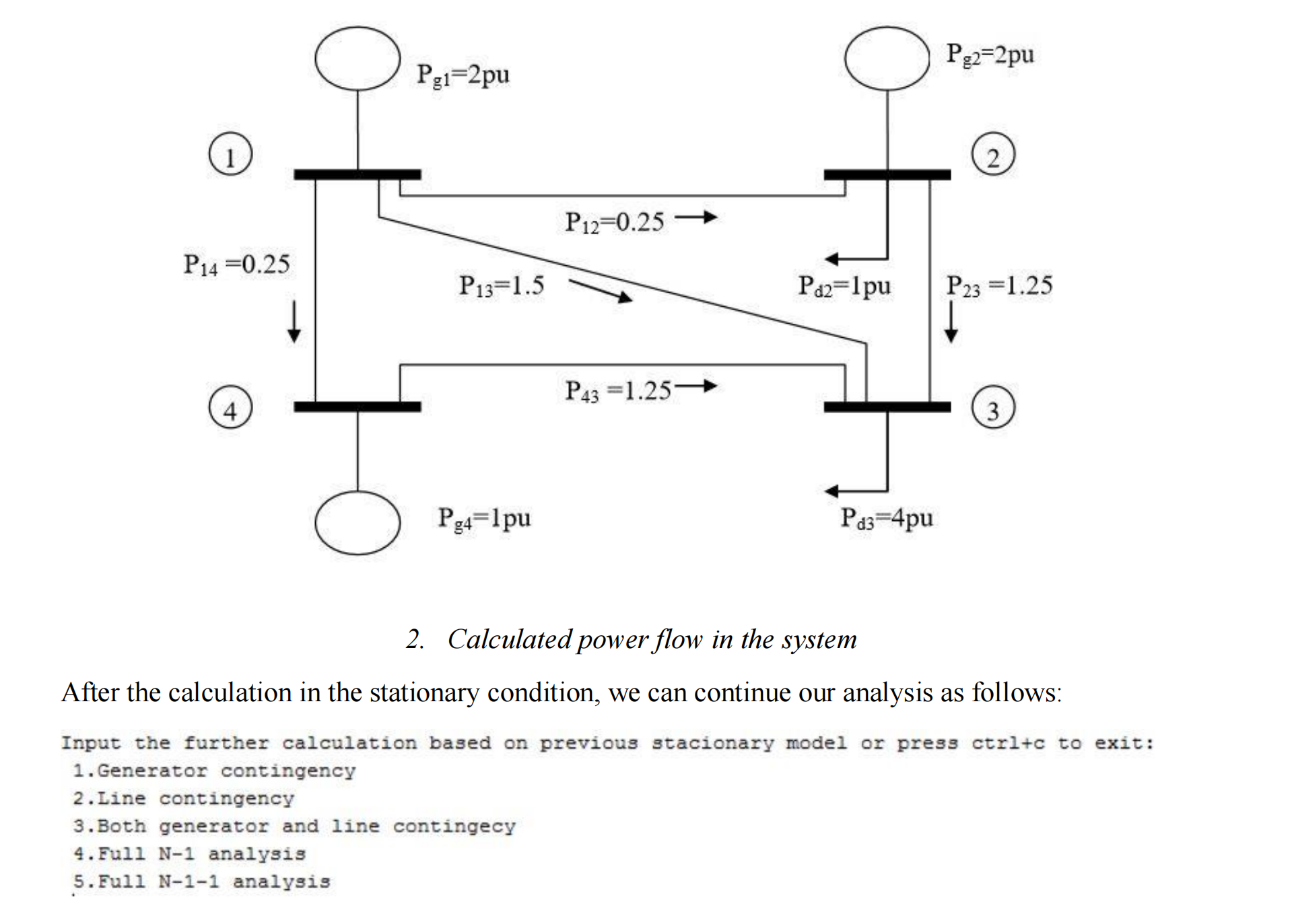
该程序接受一个感受矩阵 B=[NxN] 和注入功率 P 的向量作为输入(其中 P 的长度为 N),其中 N 是网络中的节点数。这个程序可以在单位制和绝对制中进行计算,用户可以根据需要选择计算系统。在附带的pdf文件中,详细解释了线性直流(DC)模型,并提供了使用该程序的完整说明。该代码最多可用于包含9999个节点的各种系统型号,主要是为了正确地输入感受率矩阵 B 和注入功率向量 P。当系统发生意外情况(如发电机关闭、线路关闭等)或需要进行完整的N-1或N-1-1分析时,该程序还可以进行进一步的计算。
在该程序中,感受矩阵 B 是一个关键的输入参数。它描述了网络中节点之间的连接情况和传导特性。通过结合注入功率向量 P,该程序能够计算出节点之间的电流和电压分布。这对于电力系统的稳态分析和短路计算非常有用。
在单位制中进行计算意味着使用标准单位,例如安培(A)和伏特(V),来表示电流和电压值。而在绝对制中进行计算意味着使用实际的物理量值,例如毫安(mA)和千伏(kV)。用户可以根据自己的需求选择适合的计算系统。
该程序的pdf文件提供了对线性直流模型的详细解释。该模型是一种简化的电力系统模型,可以有效地进行稳态分析。它假设电力系统中的电流和电压是线性关系,并且不考虑电源的动态响应。这个模型在电力系统工程中被广泛使用,并且在实际应用中具有很高的准确性。
使用该程序时,用户需要准确地输入感受率矩阵 B 和注入功率向量 P。感受率矩阵描述了节点之间的导纳和阻抗关系,是计算电流和电压分布的关键因素。注入功率向量表示了在每个节点注入的电力大小。通过准确地输入这些参数,该程序可以提供准确的计算结果。
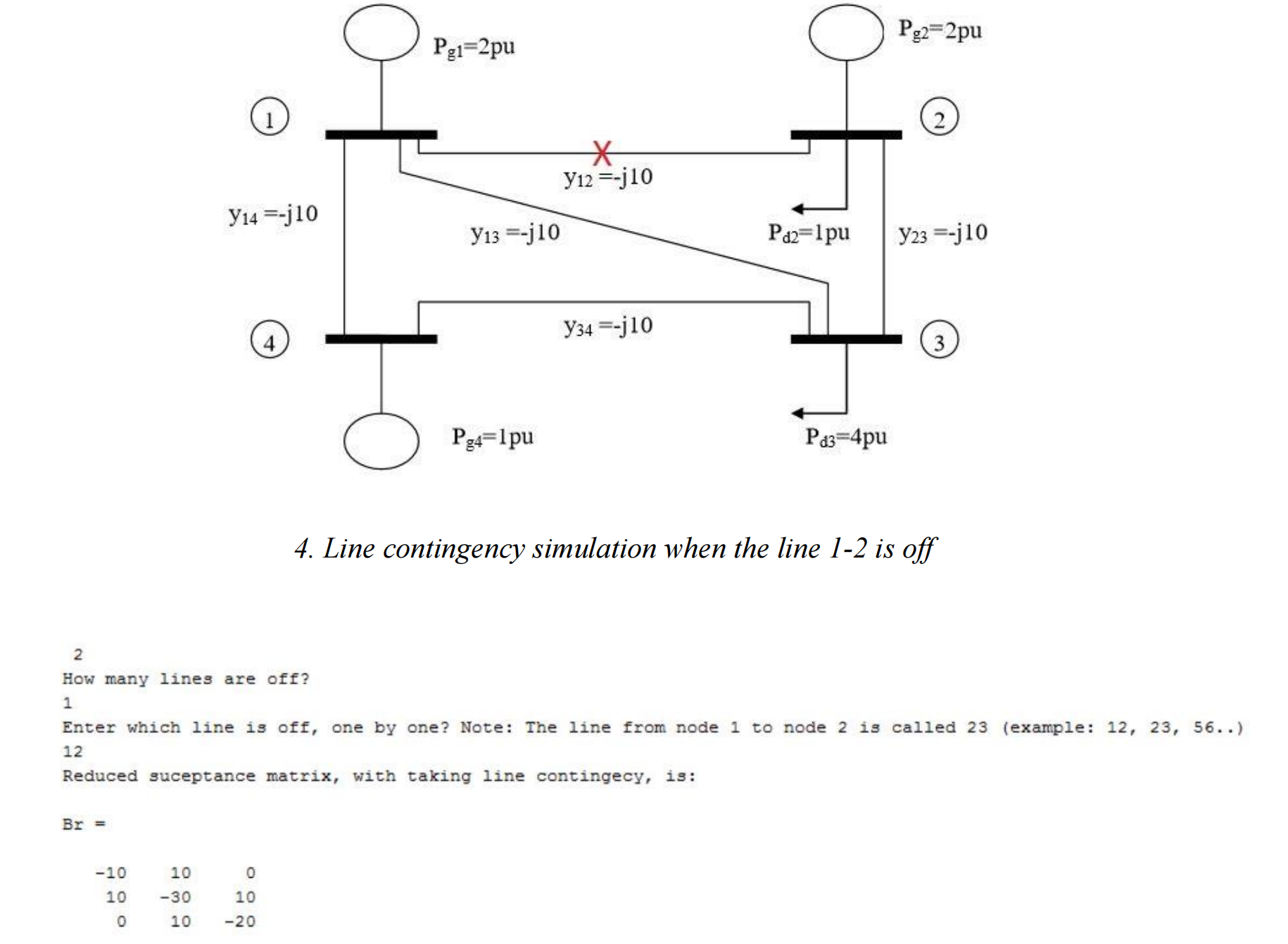
此外,该程序还具有灵活性,可以应对系统中的意外情况。当发电机关闭或线路关闭等情况发生时,该程序可以继续进行进一步的计算。这对于分析系统的鲁棒性和弹性非常重要,以确保系统在异常情况下的可靠性。
总之,该程序提供了一个强大的工具,用于计算电力系统中节点之间的电流和电压分布。通过正确输入感受率矩阵 B 和注入功率向量 P,用户可以在单位制和绝对制中进行准确的计算。该程序的pdf文件提供了对线性直流模型的详细解释和使用说明,使用户能够充分利用该程序的功能。无论是进行稳态分析还是进行进一步的N-1或N-1-1分析,该程序都能够满足用户的需求。
📚2 运行结果



部分代码:
fprintf('SOLUTION:\n');
fprintf('Angles in radians on the bus voltage phasors are:\n');
for i=1:r
fprintf('teta%.d = %.4f rad (%.4f degres) \n',i,teta(i),rad2deg(teta(i)));
end
W=index_sorting(r); %Special function for geting the unique indexes for active power values, for example 12 13 14 23 24 34 if there are 4 nodes
fprintf('Active power flows calculated by linear DC method are:\n');
for i=1:length(W)
if W(i)<100
divider=10; %if it is W=12 it means line 1 column 2 so we must divide this number with 10 to separate them to 1 and 2
elseif W(i)>=100
divider=100; %if it is W=110 it means line 1 column 10 so we must divide this number with 100 to separate them to 1 and 10
elseif W(i)>=1000
divider=1000;
elseif W(i)>=10000
divider=10000; %this means that the program is able to hande 9999 nodes
end
row=fix(W(i)/divider);
column=(rem(W(i),divider));
if B(row,column)==0 %can't divide by zero
Pa(i)=0;
else
Pa(i)=(teta(row)-teta(column))/inv(B(row,column)); % X is 1/( the corresponding element of B) so we write 'inv'
end
if unitsystem==1 && Pa(i)~=0
fprintf('Pa%d-%d = %2f p.u.\n',row,column,Pa(i));
elseif unitsystem==2 && Pa(i)~=0
fprintf('Pa%d-%d = %2f MW\n',row,column,Pa(i)*U);
end
end
answer=input('Input the further calculation based on previous stacionary model or press ctrl+c to exit:\n 1.Generator contingency\n 2.Line contingency\n 3.Both generator and line contingecy\n 4.Full N-1 analysis \n 5.Full N-1-1 analysis \n ');
if answer==1
generator_contingency
elseif answer==2
line_contingency
elseif answer==3
generator_and_line_contingency
elseif answer==4
N_1_calculation
elseif answer==5
N_1_1_calculation
end
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]武智纯.交直流电力系统概率潮流计算分析[J].中文科技期刊数据库(全文版)工程技术:00134-00134[2023-09-04].
[2]李常刚,刘玉田,张恒旭,等.基于直流潮流的电力系统频率响应分析方法[J].中国电机工程学报, 2009, 29(034):36-41.










