---

前言

1. 图的基本概念
   1.1 有向图
   1.2 无向图
   1.3 有向完全图
   1.4 无向完全图
   1.5 连通图

---

一、图的基本概念

图的定义

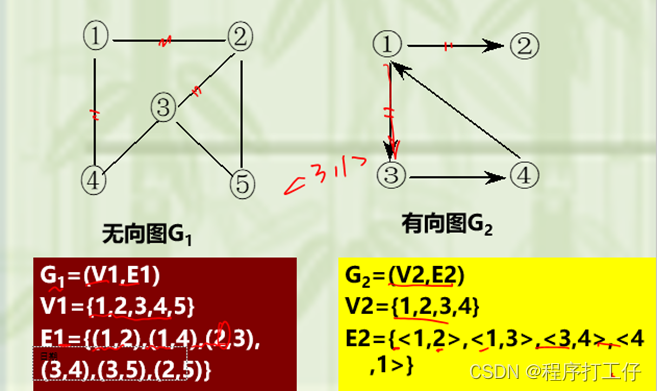
1. 图的定义：图G是顶点集V和边集E组成，记为G=(V,E)，其中V(G)表示图G中顶点有限非空集，E(G)表示图G中顶点之间关系（边）的集合，图中顶点个数也叫图的阶，图不可以是空，边集可以为空

2. 有向图：E是有向边（也叫弧）的有限集合，G是有向图，有向边记为<v,w>，顶点v到顶点w
   

3. 简单图：不存在重复边，不存在顶点到自身的边

4. 无向完全图：无向图中任意两个顶点之间都存在边称为无向完全图(有一个n个顶点的无向完全图中每个顶点到其他(n-1)个顶点都连有一条边)

5. n个顶点的无向完全图有n(n-1)/2条边
   

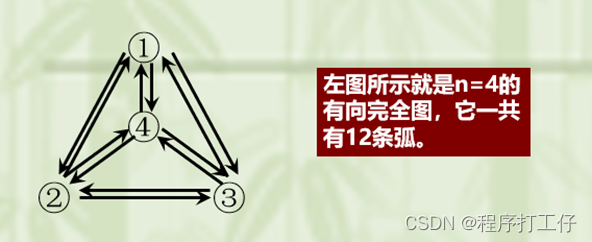
6. 有向完全图：有向图中，任意两定点间存在方向相反的两条边，称为有向完全图(在一个有n个顶点的有向完全图中每个顶点到其他(n-1)个顶点都连有一条弧)则n个顶点有n(n-1)条弧
   

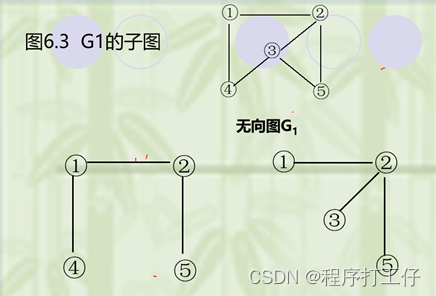
7. 子图：设有两个图G =(V,E)和G’=(V’,E’)，若V(G’)是V(G)的子集，且E(G’)是E(G)的子集，则称G’是G的子图(Subgraph)。
   

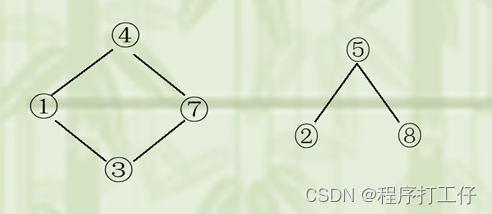
8. 连通、连通图和连通分量：无向图中，顶点v到w有路径存在，则v和w是连通的，任意两个顶点间都存在路径则是连通图；无向图中极大连通子图称为连通分量，若有n个顶点，并且小于n-1条边，则必为非连通图；边最少(n-1条)即构成一个树
   

9. 强连通图、强连通分量：有向图中，从顶点v到w和从w到v都有路径，则称两顶点是强连通的，任意一对顶点都是强连通的则是强连通图；边最少即构成有向环

10. 非强连通图的每一个极大强连通子图称为G的生成树

11. 生成树：连通图生成树是包含全部顶点的一个极小连通子图，顶点为n个，生成树有n-1条边(包含无向图G所有顶点的极小连通子图，成为生成树)

12. 极小连通子图：该子图是G的连通子图，在该子图中删除任何一条边，子图都不在连通

13. 顶点的度、入度和出度：度是以该顶点为一个端点的边的数目；

14. 对于无向图，顶点度是依附于该顶点边的条数，全部顶点的度之和等于边数的两倍；

15. 有向图入度是以顶点v为终点的有向边的数目，出度是以顶点v为起点的有向边的数目，顶点度等于出度和入度之和，有向图全部顶点的入度之和和出度之和相等且等于边数

16. 边的权和网：有些图， 对应每条边有一相应的数值，这个数值叫做该边的权(Weight)。边上带权的图称为带权图，也称为网络。

17. 路径、路径长度和回路：一个顶点到另一顶点全部路径过程，路过边数称为路径长度，第一个顶点和最后一个顶点相同的叫回路；一个图有n个顶点，并且有大于n-1条边，此图一定有环

18. 距离：从顶点v到w最短路径若存在，则叫距离

19. 简单路径：顶点不重复出现；除第一个和最后一个顶点外，其余顶点不重复出现的回路叫简单回路

20. 有向树：一个顶点入度为0，其余入度全为1，则称此有向图为有向树

总结

1. 图的基本概念
   1.1 有向图
   1.2 无向图
   1.3 有向完全图
   1.4 无向完全图
   1.5 连通图