二叉树的遍历

Ⅰ、二叉树基本介绍

1.1、二叉树的定义

二叉树（binary tree）是指树中节点的度不大于2的有序树，它是一种最简单且最重要的树。

二叉树的递归定义为：二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树。

1.2、特殊的二叉树

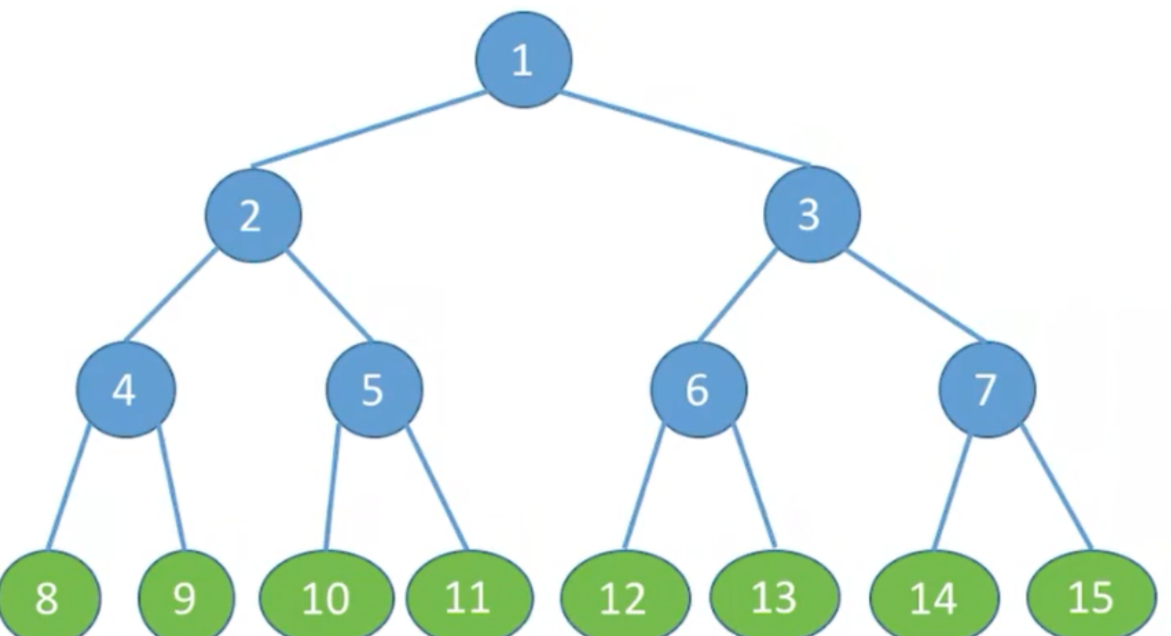
1、满二叉树：如果一棵二叉树只有度为0的节点和度为2的节点，并且度为0的节点在同一层上，则这棵二叉树为满二叉树。

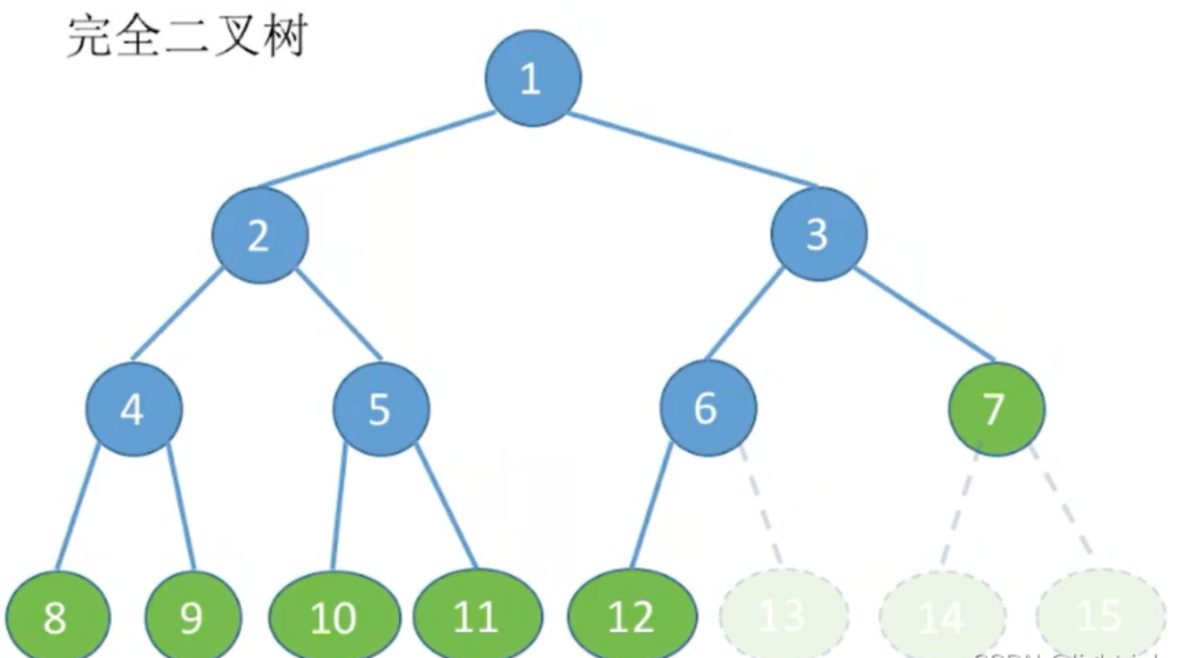
2、完全二叉树：深度为k，有n个节点的二叉树当且仅当其每一个节点都与深度为k的满二叉树中编

号从1到n的节点一一对应时，称为完全二叉树。

完全二叉树的特点是叶子节点只可能出现在层序最大的两层上，并且某个节点的左分支下子孙的最

大层序与右分支下子孙的最大层序相等或大1 。

Ⅱ、二叉树的性质

性质1：二叉树的第i层上至多有2i-1（i≥1）个节点。

性质2：深度为h的二叉树中至多含有2h-1个节点 。

性质3：若在任意一棵二叉树中，有n0个叶子节点，有n2个度为2的节点，则必有n0=n2+1 。

性质4：具有n个节点的满二叉树深为log2n+1。

性质5：若对一棵有n个节点的完全二叉树进行顺序编号（1≤i≤n），那么，对于编号为i（i≥1）的节点：

当i=1时，该节点为根，它无双亲节点。

当i>1时，该节点的双亲节点的编号为i/2 。

若2i≤n，则有编号为2i的左节点，否则没有左节点。

若2i+1≤n，则有编号为2i+1的右节点，否则没有右节点。

Ⅲ、二叉树的四种遍历方式

如果二叉树中元素数目为n。这四种遍历算法的空间复杂性均为O (n)，时间复杂性为O(n)。

3.1、二叉树的前序遍历

遍历顺序：跟左右

前序遍历首先访问根结点然后遍历左子树，最后遍历右子树。在遍历左、右子树时，仍然先访问根

节点，然后遍历左子树，最后遍历右子树。

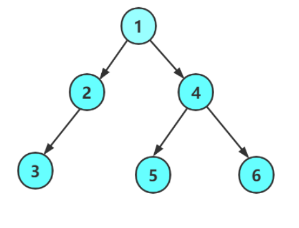
这个二叉树前序遍历的结果是：1 2 3 4 5 6

但是实际上是：1 2 3 null null null 4 5 null null 6 null

我们为了看上去方便就省去了null.

代码实现：

void PrevOrder(BTNode* root) {
	if (root == NULL) {
		printf("NULL ");

		return;
	}

	printf("%d ", root->val);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

3.2、中序遍历

遍历顺序：左根右

中序遍历（LDR）是二叉树遍历的一种，也叫做中根遍历、中序周游。在二叉树中，中序遍历首先

遍历左子树，然后访问根结点，最后遍历右子树。

中序遍历结果：3 2 1 5 4 6

实际上的结果应该是：null 3 null 2 null 1 null 5 null 4 null 6 null

代码实现：

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	InOrder(root->left);
	printf("%d ", root->val);
	InOrder(root->right);
}

3.3、后序遍历

遍历顺序：左右跟

后序遍历首先遍历左子树，然后遍历右子树，最后访问根结点，在遍历左、右子树时，仍然先遍历

左子树，然后遍历右子树，最后遍历根结点。

后续遍历结果：3 2 5 6 4 1

实际上应该是：null null 3 null 2 null null 5 null null 6 4 1

代码实现：

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->val);
}

3.4、层次遍历

遍历顺序：一层一层的遍历

二叉树的层次遍历，顾名思义就是指从二叉树的第一层（根节点）开始，从上至下逐层遍历，

同一层中，则按照从左到右的顺序对节点逐个访问。在逐层遍历过程中，按从顶层到底层的次序访

问树中元素，在同一层中，从左到右进行访问。

层次遍历结果：1 2 4 3 5 6

实际遍历结果：1 2 4 3 null 5 6 null null null null null null

代码实现：

void levelorder(BinaryTree *tree)
{
    Queue q = initQueue();
    BinaryTree *temp = tree;
    put(&q, temp);
    while (!IsEmptyQueue(q))
    {
        temp = get(&q);
        visited(temp);
        if (temp->left != NULL)
            put(&q, temp->left);
        if (temp->right != NULL)
            put(&q, temp->right);
    }
}

Ⅳ、二叉树求节点

4.1、求二叉树总节点个数

方法一

我们惯用的方式，就是创建一个变量Size，然后每遍历一个节点Size++。

这种方式有很大的局限性，就是我们在遍历二叉树时采用的是递归的方式，如果把Size放到函数里面就会出现每次调用时Size都是同一个值，没办法累加。

这里我们可以采用静态函数 stati来修饰Size,这样Size只被调用一次，就可以达到累加的效果。

看代码：

int TreeSize(BTNode* root)
{
	static int size = 0;
	if (root == NULL)
		return 0;
	else
		++size;

	TreeSize(root->left);
	TreeSize(root->right);

	return size;
}

这样我们的得到的结果就是：6。

但是：当我们再次调用这个函数时我们会不会还得到结果6呢？答案是不会，他会返回12。因为我们刚才提到静态变量修饰的Size时，Size在整个程序中只会被调用一次。所以这种方式有很大的局限性。我们不妨换个思路来解决

方法二

我们还是采用递归的方式，当遍历到叶子节点是我们就让他返回1，一层一层的往上返回，最终在加上1（根节点），我们是不是就可以得到我们整棵树的节点个数了呢？

看代码：

int TreeSize(BTNode* root)
{
	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

4.2、求二叉树叶子结点的个数

有了上面求二叉树总节点个数方法二的铺垫，这个问题也就很容易想到了。

这里我们要怎么确定一个节点时叶子节点呢？很简单没有左右孩子的节点就是叶子节点

我们可以遍历整个二叉树，遇到叶子节点就返回1，直到遍历到最后我们返回0，把他们全都累加起来，最后结果就是我们想要的叶子结点的个数。

看代码：

int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;

	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}

	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

4.3、求第K层节点的个数

这个问题相比于上面两个要复杂一点，首先我们要先解决如何遍历到第K层。

若要求第三层节点的个数：第一层相和第三层差2层，第二层和第三层差1层，第三层和第三层差0层......当k=1时证明就在第k层，我们就返回这个第K层的节点为1

我们可以得出一个结论：当前树的第K层 = 左子树的第K-1层 + 右子树的第K-1层

接下来我们来看代码：

int TreeKLevel(BTNode* root, int k)
{
	assert(k > 0);

	if (root == NULL)
		return 0;

	if (k == 1)
	{
		return 1;
	}

	return TreeKLevel(root->left, k - 1)
		+ TreeKLevel(root->right, k - 1);
}

Ⅴ、二叉树相关练习

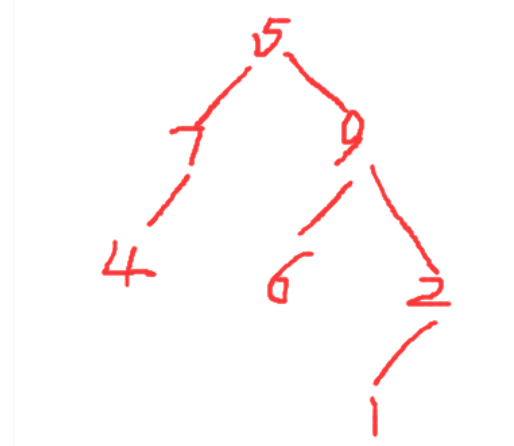
1、已知二叉树的前序遍历为5 7 4 9 6 2 1，中序遍历是4 7 5 6 9 1 2则该二叉树的后序遍历是什么？

答案：4 7 6 1 2 9 5

解析：

通过前序遍历找到子树的根，在中序遍历中找到根的位置，然后确定根左右子树的区间，即根的左侧为左子树中所有节点，根的右侧为右子树中所有节点。

故：根为： 5

5的左子树：4 7   5的右子树： 6 9  1  2

5的左子树的根为: 7  5的右子树的根为：9

7的左子树: 4 7的右：空  9的左子树：6  9的右子树：2

这棵树的结构是：

2、如果一颗二叉树的前序遍历的结果是ABCD，则满足条件的不同的二叉树有（）种

答案：14

解析：

首先这棵二叉树的高度一定在3~4层之间:

三层：

A(B(C,D),()), A((),B(C,D)), A(B(C,()),D), A(B((),C),D),

A(B,C(D,())), A(B,C((),D))

四层：

如果为四层，就是单边树，每一层只有一个节点，除过根节点，其他节点都有两种选择，在上层节点的左边还是右边，所以2*2*2共8种

总共为14种。

也可以由公式的来：，这里的n指的是二叉树结点的个数（5*6*7*8）/（1*2*3*4）/（n+1）

答案也是14。

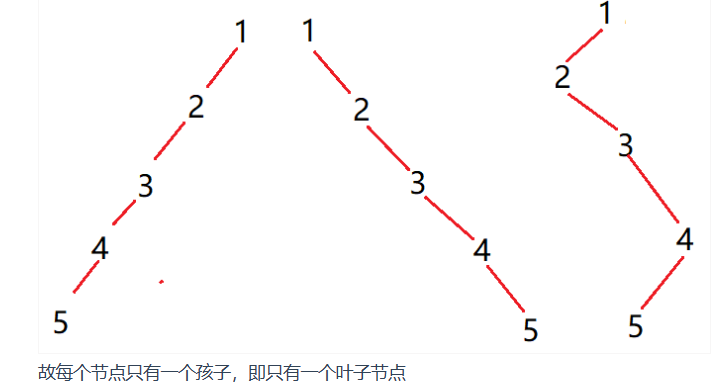
3、一棵非空的二叉树的先序遍历序列与后序遍历序列正好相反，则该二叉树一定满足（）

答案：只有一个叶子节点

解析：

前序遍历：根左右

后序遍历：左右根

从二叉树前序和后序遍历结果规则中可以看出，如果树中每个节点只有一个孩子时，遍历结果肯定是反的

比如下面这前序和中序序列所构成的树的结构:

结语：这篇文章讲到这也就结束了，如有疑问或者质疑，请在评论区发出来，我会尽全力帮大家解决，成长的路上少不了你们的支持，你们的三连是我进步最大的动力，还望大佬们多多支持，一起加油！共勉！