LeetCode：2603. 收集树中金币详解（2023.9.21 C++）

2603. 收集树中金币

题目描述：

给你一个 n 个节点的无向无根树，节点编号从 0 到 n - 1 。给你整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间有一条边。再给你一个长度为 n 的数组 coins ，其中 coins[i] 可能为 0 也可能为 1 ，1 表示节点 i 处有一个金币。

一开始，你需要选择树中任意一个节点出发。你可以执行下述操作任意次：

收集距离当前节点距离为 2 以内的所有金币，或者
移动到树中一个相邻节点。

你需要收集树中所有的金币，并且回到出发节点，请你返回最少经过的边数。

如果你多次经过一条边，每一次经过都会给答案加一。

示例 1：

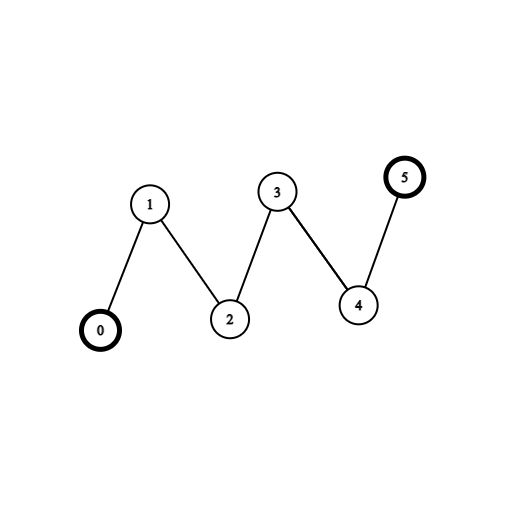
输入：coins = [1,0,0,0,0,1], edges = [[0,1],[1,2],[2,3],[3,4],[4,5]]
输出：2
解释：从节点 2 出发，收集节点 0 处的金币，移动到节点 3 ，收集节点 5 处的金币，然后移动回节点 2 。

示例 2：

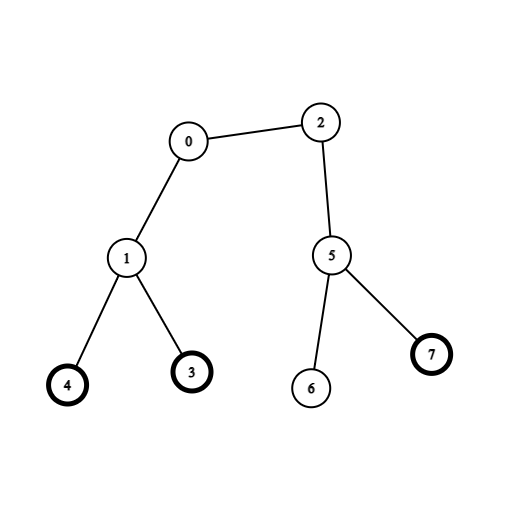
输入：coins = [0,0,0,1,1,0,0,1], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[5,6],[5,7]]
输出：2
解释：从节点 0 出发，收集节点 4 和 3 处的金币，移动到节点 2 处，收集节点 7 处的金币，移动回节点 0 。

提示：

n == coins.length
1 <= n <= 3 * 104
0 <= coins[i] <= 1
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
ai != bi
edges 表示一棵合法的树。

实现代码与解析：

拓扑 + bfs

class Solution {
public:
    vector<int> h = vector<int>(30010, -1), e = vector<int>(60010, 0), ne = vector<int>(60100, 0), d = vector<int>(30010, 0);
    int idx = 0;
    void add(int a, int b)
    {
        e[idx] = b; ne[idx] = h[a]; h[a] = idx++;
    } 

    int collectTheCoins(vector<int>& coins, vector<vector<int>>& edges) {
        

        int n = coins.size(); // 结点个数
        int rest = n; // 剩余的结点 rest翻译剩余

        for (auto t: edges)
        {
            int a = t[0];
            int b = t[1];
            add(a, b), add(b, a); // 加无向边
            d[a]++, d[b]++; // 两个结点 入度++
        }

        queue<int> q;
        // 删除树中 无金币 的叶子结点
        for (int i = 0; i < n; i++) 
            if (d[i] == 1 && !coins[i]) q.push(i); // 无向边，入度为1的是叶子节点，要和有向的区分开
        while (q.size())
        {
            int t = q.front();
            d[t]--; // d[t]-- 此结点从1变为0 相当于删除此节点和边
            rest--; // 剩余结点--
            q.pop();
            for (int i = h[t]; ~i; i = ne[i])
            {
                int j = e[i];
                d[j]--; // 相邻结点 入度--
                if (d[j] == 1 && !coins[j]) q.push(j); // 入度为1的继续入队，因为有可能有新0金币结点 因为删除 变为叶子结点
            }
        }

        // 拓扑（拓扑排序中的两个去除环节 执行两次） 去除叶子结点 两次
        for (int i = 0; i < 2; i++)
        {
            queue<int> qq;

            for (int i = 0; i < n; i++)
                if (d[i] == 1) qq.push(i); // 叶子结点入队
            
            while(qq.size())
            {
                int t = qq.front();
                d[t]--;
                qq.pop();
                rest--;
                for (int i = h[t]; ~i; i = ne[i])
                {
                    int j = e[i];
                    d[j]--;
                } 
            }
        }

        return rest == 0 ? 0 : 2 * (rest - 1);
    }
};

原理思路：

首先去掉无金币的叶子结点，因为无金币的叶子结点是不需要收集的，收集绝对会浪费步数，以它为起点也会浪费步数，所以可以直接删除掉（连同它相连的边），直到叶子结点中没有无金币的。

然后从叶子节点一层一层往剥，举个例子，比如一个三层的饼干，如果左右扩散为1，肯定是要选最中间的那层，就可以获得整个饼干（也就是去掉外面两侧，剩的那一层），如果是4层饼干，那么我们就要选中间两层（也就是去掉外面两侧，剩下的那二层）。

扩散为2，或者更多层数，也是同理，就是逆像思维从外一层一层往里剥（也就是拓扑），最后剩下的就一定是我们需要遍历。

最后剩 n 个结点的话，需要全部走完，n个节点 n - 1 条边，每条边走两次才能回到原位，所以答案就为 2 * (n - 1)。

核心思想：删除没有金币的叶子节点，然后连续两次删除所有叶子节点。最终结果基于树中剩余节点的数量计算得出。

代码的话，其实思想明白了就很好写了，就是基础的bfs和拓扑代码，如果不会拓扑可以看看我之前写的拓扑排序的写法和有关的题。

拓扑排序详解（带有C++模板）_Cosmoshhhyyy的博客-CSDN博客

LeetCode：207. 课程表、210. 课程表 II（拓扑排序 C++）_Cosmoshhhyyy的博客-CSDN博客

注意点：这里是无向图，我这种图的邻接表写法，需要二倍的边的个数，而且平时拓扑都是为0的时候入队，这里是1，因为是无向图嘛。最后如果没有节点，就返回0。