1.题目

给你一个 n 个节点的无向无根树，节点编号从 0 到 n - 1 。给你整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间有一条边。再给你一个长度为 n 的数组 coins ，其中 coins[i] 可能为 0 也可能为 1，1 表示节点 i 处有一个金币。一开始，你需要选择树中任意一个节点出发。你可以执行下述操作任意次：

• 收集距离当前节点距离为 2 以内的所有金币，或者
• 移动到树中一个相邻节点。

你需要收集树中所有的金币，并且回到出发节点，请你返回最少经过的边数。如果你多次经过一条边，每一次经过都会给答案加一。

示例 1：

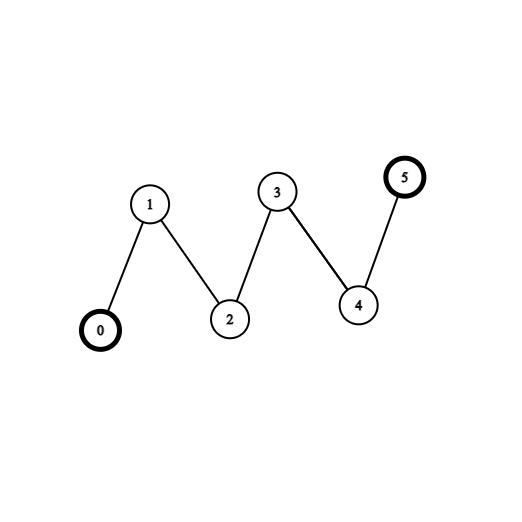
输入：coins = [1,0,0,0,0,1], edges = [[0,1],[1,2],[2,3],[3,4],[4,5]]
输出：2
解释：从节点 2 出发，收集节点 0 处的金币，移动到节点 3 ，收集节点 5 处的金币，然后移动回节点 2。

示例 2：

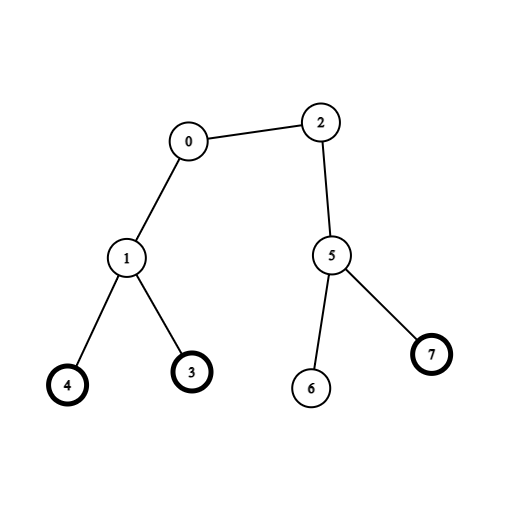
输入：coins = [0,0,0,1,1,0,0,1], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[5,6],[5,7]]
输出：2
解释：从节点 0 出发，收集节点 4 和 3 处的金币，移动到节点 2 处，收集节点 7 处的金币，移动回节点 0 。

提示：
n == coins.length
1 <= n <= 3 * 10⁴
0 <= coins[i] <= 1
edges.length == n - 1
edges[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
edges 表示一棵合法的树。

2.思路

（1）两次拓扑排序
思路参考本题官方题解。

3.代码实现（Java）

//思路1————两次拓扑排序
class Solution {
    public int collectTheCoins(int[] coins, int[][] edges) {
        int n = coins.length;
        //图的邻接表
        List<Integer>[] graph = new ArrayList[n];
        for (int i = 0; i < n; ++i) {
            graph[i] = new ArrayList<>();
        }
        //计算每个节点的度
        int[] degree = new int[n];
        for (int[] edge : edges) {
            int x = edge[0], y = edge[1];
            graph[x].add(y);
            graph[y].add(x);
            ++degree[x];
            ++degree[y];
        }
        //将入度为 1 且无金币的叶子节点放入队中
        Queue<Integer> queue = new ArrayDeque<>();
        for (int i = 0; i < n; ++i) {
            if (degree[i] == 1 && coins[i] == 0) {
                queue.offer(i);
            }
        }
        int rest = n;
        while (!queue.isEmpty()) {
            int u = queue.poll();
            --degree[u];
            --rest;
            for (int v : graph[u]) {
                --degree[v];
                if (degree[v] == 1 && coins[v] == 0) {
                    queue.offer(v);
                }
            }
        }
        //删除树中所有的叶子节点，连续删除 2 次
        for (int x = 0; x < 2; ++x) {
            queue = new ArrayDeque<Integer>();
            for (int i = 0; i < n; ++i) {
                if (degree[i] == 1) {
                    queue.offer(i);
                }
            }
            while (!queue.isEmpty()) {
                int u = queue.poll();
                --degree[u];
                --rest;
                for (int v : graph[u]) {
                    --degree[v];
                }
            }
        }
        return rest == 0 ? 0 : (rest - 1) * 2;
    }
}