目录
文章正式开始，让我们一起学习树吧！！
一：树的概念
树是一种非线性结构 ，与我们前面所学的顺序表与链表不同，数据元素的对应是1对多的关系，只有一个根结点，且除了根节点其它的结点有且仅有1个前驱结点(父结点)。
我们可以将一棵树看作由很多个结构相似的子树组成，所以树是递归定义的。
注意：在树形结构中子树不能出现相交，简单的来说就是一棵树中不能出现闭合的结构。
1.1：树的相关概念
节点的度：一个结点含有子树的个数称为该节点的度。
叶结点或终端结点：度为0的结点，称为叶节点。
非终端节点或分支结点：度不为0的结点。
双亲结点或父节点：结点的前驱结点曾为它的父节点或双亲结点。
兄弟结点：具有相同父节点的结点。
树的度：树中最大节点的度称为树的度。
节点的层次：从根开始定义起，根为第一层，子节点自增。
树的高度：树中节点的最大层次。
堂兄弟结点：双亲在同一层的结点。
结点的祖先：从根到该节点所经分支上的所有节点。
子孙：在某一棵树中，选定根节点之后所有的其它节点都是该节点的子孙。
森林：由m(m>0)棵互不相交的树的集合称为森林。
1.2：树的结构(表示)
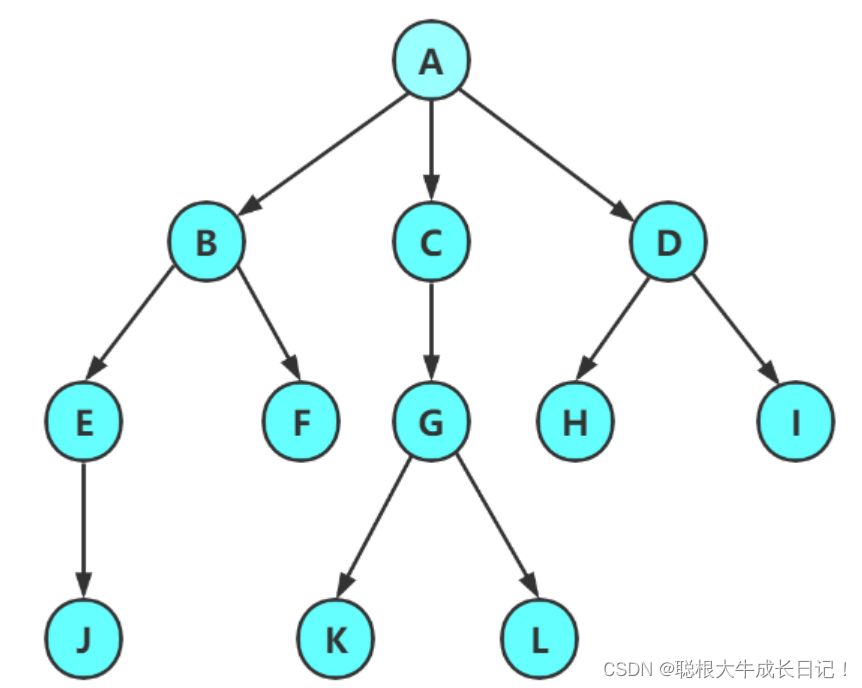
我们应该如何来表示这棵树呢？
因为我们不仅要保留节点的值，还需要保留结点与结点的关系。
在实际中有许许多多的方法可以用来表示树的结构，我们来介绍一种非常牛逼的方法，叫做孩子兄弟法。
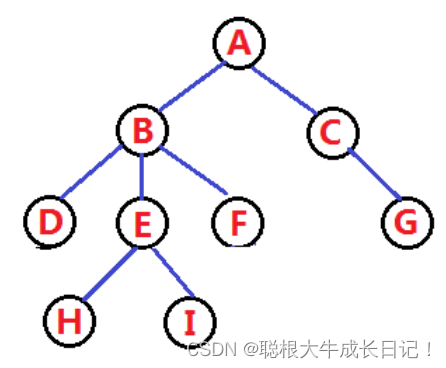
比如我们想要表示上述的这棵树。
我们定义一个结点：
struct TreeNode
{
int val;
struct TreeNode* FirstChild;
struct TreeNode* brother;
};用图来表示---->
其实在我们电脑中经常会使用到树这个数据结构，比如我们的磁盘放置文件的结构就是这样的。还有在我们Linux系统上。
二：二叉树相关概念与结构
2.1：概念
二叉树：由根节点与左右子树构成，且节点的度不超过2。
任何二叉树都是由一下几种情况复合而成的->
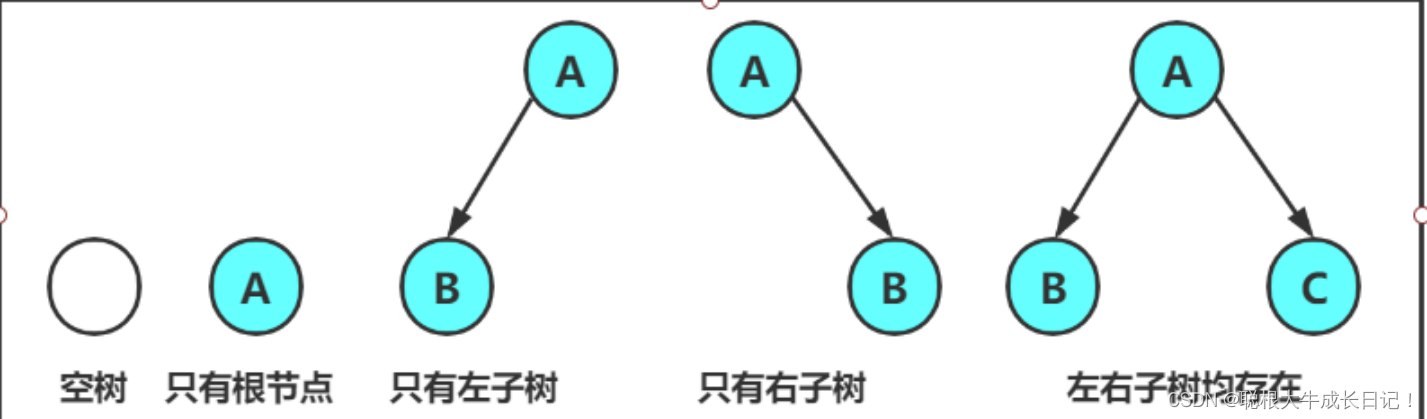
对于任何一颗二叉树我们都可以将他看成三个部分：根左子树右子树，看成这样的结构的时候我们有利于采用分治的思想解决二叉树的有关问题。
二叉树的子树有左右之分，不能跌倒它们的次序，所以二叉树是有序树。
2.2特殊的二叉树
在二叉树中有两种特殊的树：满二叉树与完全二叉树
满二叉树：一个二叉树中，每一层的结点的个数都达到了最大值，假设高度为h，那么我们可以通过推理可以得出结点的个数为：2^h-1。
如图：
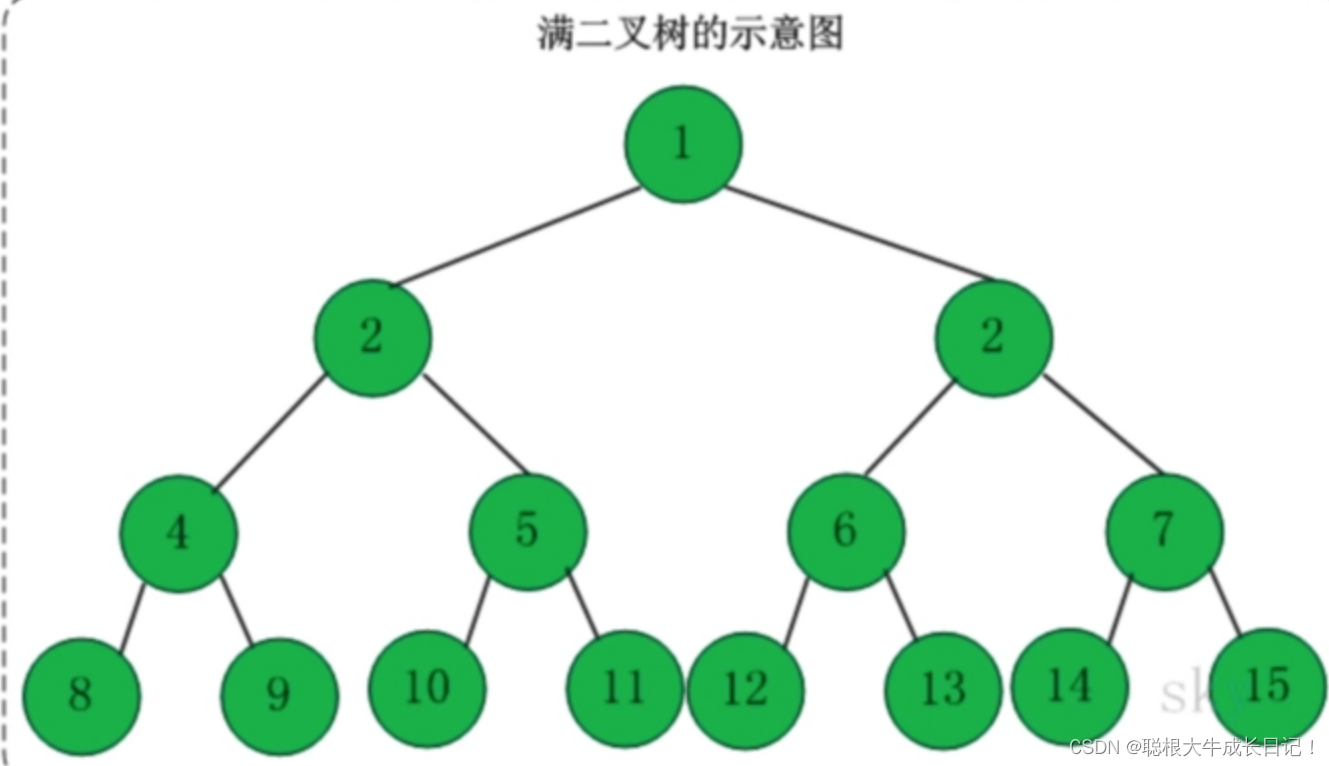
完全二叉树：假设高度为h，在一棵二叉树中，前h-1层是满二叉树，且第h层结点是连续的
它的结点的范围为：[2^(h-1),2^h-1].
2.3：二叉树的性质
规定根节点的层数为1
1：一棵非空二叉树的第i层最多有2^(h-1)个结点
2：深度为h的二叉树，最多有2^h-1个结点。
3:对于任何一颗二叉树度为0结点的个数等于度为2结点的个数加1：n0=n2+1;
4:具有n个结点的满二叉树的深度为：h=log(n+1).
三：二叉树的链式结构
这里我们采用简单一点的二叉树结构，我们手动的创建二叉树
代码如下：
定义结构的代码：
typedef int TreeDataType;
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
TreeDataType val;
}TRNode;
TRNode* node1=BuyTreeNode(1);
TRNode* node2= BuyTreeNode(2);
TRNode* node3 = BuyTreeNode(3);
TRNode* node4 = BuyTreeNode(4);
TRNode* node5 = BuyTreeNode(5);
TRNode* node6 = BuyTreeNode(6);
node1->left = node2;
node2->left = node3;
node1->right = node4;
node4->left = node5;
node4->right = node6;3.1二叉树的遍历
二叉树的遍历是我们学习二叉树最简单的操作，有三种遍历方式且我们遍历一个结点只操作一次。
前序遍历：访问的方式为：根 左子树 右子树
代码如下：
void prevOrder(TRNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%d ", root->val);
prevOrder(root->left);
prevOrder(root->right);
}接下来我们采用递归展开图的方式来详细讲解这段代码的意思。
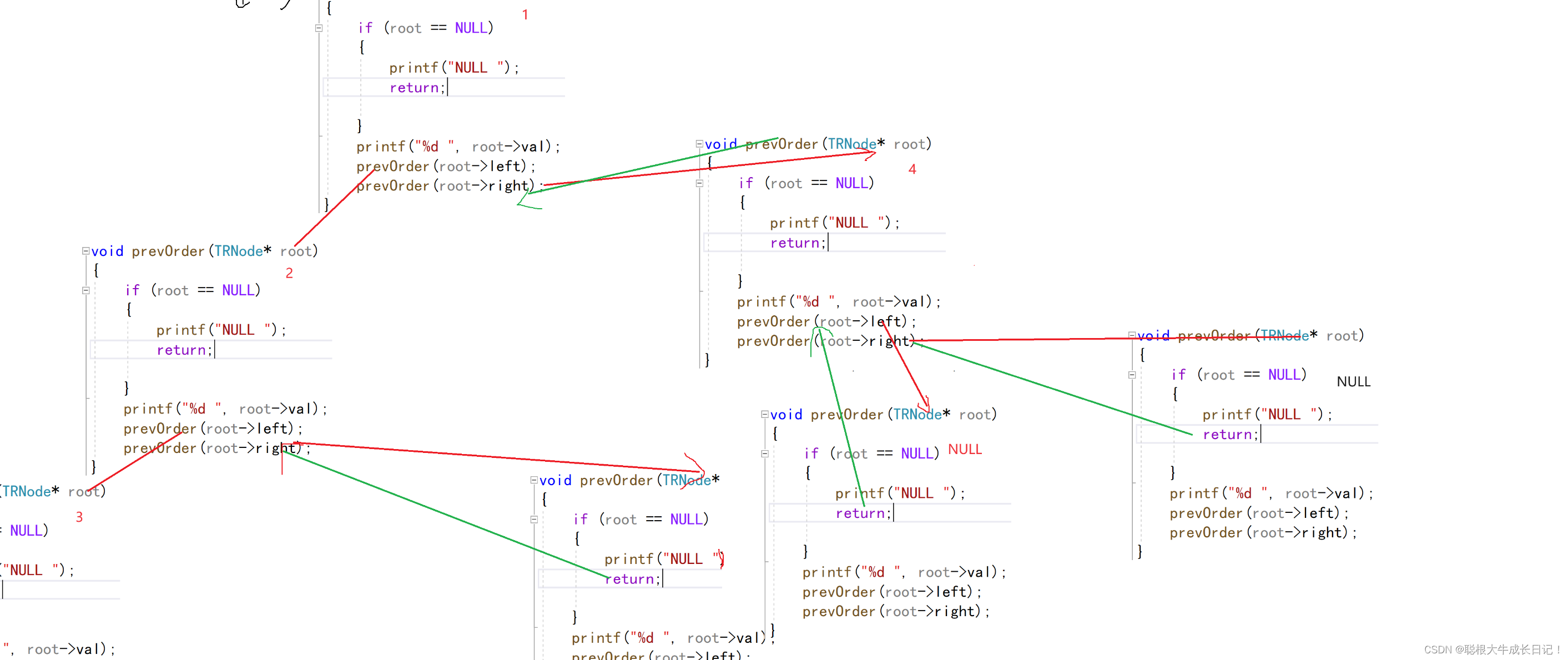
中序遍历：左子树 根 右子树
代码：
void InOrder(TRNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%d ", root->val);
InOrder(root->right);
}这里就不详细讲解了。
后序：左子树 右子树 根
void postOrder(TRNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
postOrder(root->left);
postOrder(root ->right);
printf("%d ", root->val);
}本章分享完毕，感谢大家的观看。
