【C++ 学习 ㉒】- 超详解 AVL 树的插入、平衡调整以及删除（含源代码）

2023-09-21 21:34:27

目录

一、AVL 树的概念

二、AVL 树节点的定义

三、AVL 树的插入

四、AVL 树的平衡调整

五、AVL 树的删除

六、AVL 树的实现

6.1 - AVL.h

6.2 - test.cpp

 

一、AVL 树的概念

二叉搜索树查找算法的性能取决于二叉树搜索树的形状，而二叉搜索树的形状则取决于数据集。如果数据呈有序排列，则二叉搜索树为单支树，查找的时间复杂度为 O(n)；反之，如果二叉搜索树的形状合理，则查找速度较快，查找的时间复杂度为 O(log_2^n)。事实上，树的高度越小，查找速度越快，因此，希望二叉树的高度尽可能小。下面将讨论一种特殊类型的二叉搜索树，称为平衡二叉树（Balanced Binary Tree 或 Height-Balanced Tree），因由前苏联数学家 Adelson-Velskii 和 Landis 提出，所以又称 AVL 树。

平衡二叉树或者是空树，或者是具有如下特征的二叉搜索树：

  1. 左子树和右子树的高度之差的绝对值不超过 1。

  2. 左子树和右子树也是平衡二叉树。

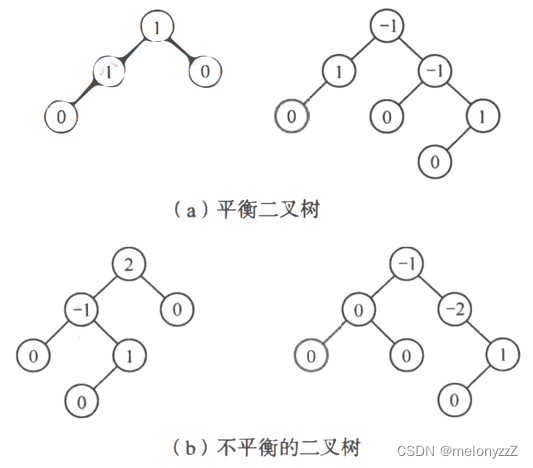
若将二叉树上节点的平衡因子（BF, Balance Factor）定义为该节点左子树和右子树的高度之差，则平衡二叉树上的所有节点的平衡因子只可能是 -1、0 和 1。只要二叉树上有一个节点的平衡因子的绝对值大于 1，则该二叉树就是不平衡。

例如，下面图 (a) 所示为两棵平衡二叉树，图 (b) 所示则为两棵不平衡的二叉树，节点中的值为该结点的平衡因子。

因为 AVL 树上任何节点的左右子树的高度之差都不超过 1，则可以证明它的深度和 log_2^n 是同数量级的（其中 n 为节点个数）。由此，其查找的时间复杂度是 O(log_2^n)。

二、AVL 树节点的定义

template<class K, class V>
struct AVLNode
{
    AVLNode<K, V>* _left;
    AVLNode<K, V>* _right;
    AVLNode<K, V>* _parent;
    std::pair<K, V> _kv;
    int _bf;
​
    AVLNode(const std::pair<K, V>& kv = std::pair<K, V>())
        : _left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0)
    { } 
};

三、AVL 树的插入

当新增的节点 *cur（指向节点的指针为 cur） 插入到其双亲节点 *parent（指向节点的指针为 parent）的左边时，双亲节点的平衡因子 +1；反之，当新增的节点插入到其双亲节点的右边时，双亲节点的平衡因子 -1。

  1. 若双亲节点的平衡因子原来为 -1 或者 1，在它的左边或者右边插入新增的节点后，它的平衡因子变为 0。由于以 *parent 为根节点的子树的高度没有发生变化，因此也不会影响除 *parent 以外的其它祖先节点的平衡因子，插入完成。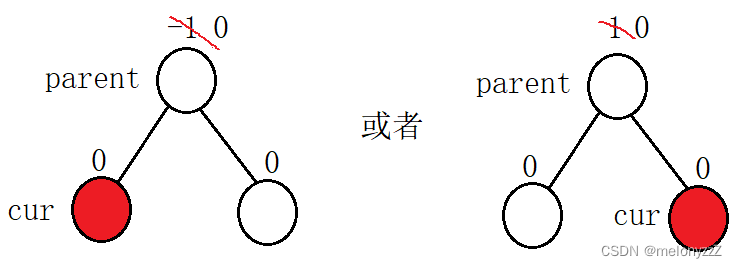

  2. 若双亲节点的平衡因子原来为 0，在它的左边或者右边插入新增的节点后，它的平衡因子变为 1 或者 -1。由于以 *parent 为根节点的子树的高度增高了 1，此时也就会影响其它祖先节点的平衡因子，需要往上更新。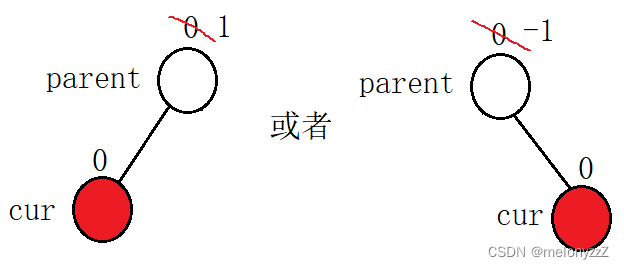

    往上更新其它祖先节点的平衡因子的方式和一开始插入新增节点 *cur 时更新其双亲节点 *parent 的平衡因子的方式是一样的，即如果 *cur 在祖先节点的左子树中，则祖先节点的平衡因子 +1；如果 *cur 在祖先节点的右子树中，则祖先节点的平衡因子 -1。

    • 如果祖先节点的平衡因子被更新为 0，则说明更新完成了，也意味着插入完成了。

    • 如果祖先节点的平衡因子被更新为 1 或者 -1，则说明还需要继续往上更新，直到某个祖先节点的平衡因子被更新为 0，或者直到更新完根节点，当根节点的平衡因子被更新为 0、1 或者 -1 时，意味着更新和插入也都完成了。

    • 如果祖先节点的平衡因子被更新为 2 或者 -2（即其较高的子树增高了），就需要对以该节点为根节点的子树（称为最小不平衡子树）做平衡调整来恢复平衡。

四、AVL 树的平衡调整

假设最小不平衡子树的根节点为 A，则失去平衡后进行调整的规律可归纳为下列 4 种情况。

  1. LL 型：由于在 A 左子树根节点的左子树上插入节点，A 的平衡因子由 1 增至 2，致使以 A 为根节点的子树失去平衡，则需进行一次向右的顺时针旋转操作。

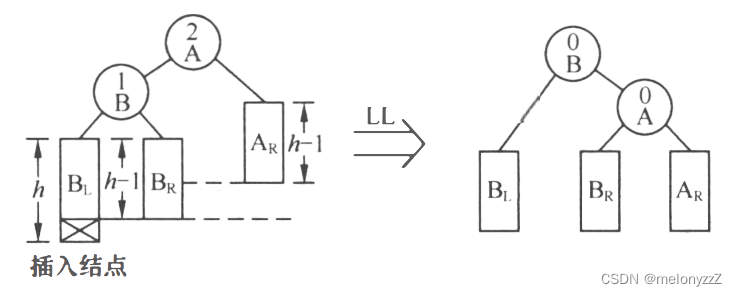
    void LL(Node* pA)
{
    Node* pB = pA->_left;
    Node* pBR = pB->_right;
​
    pA->_left = pBR;
    if (pBR)
        pBR->_parent = pA;
​
    pB->_right = pA;
    Node* tmp = pA->_parent;
    pA->_parent = pB;
    pB->_parent = tmp;
​
    if (tmp == nullptr)  // 或者 _root == pA
    {
        _root = pB;
    }
    else
    {
        if (tmp->_left == pA)
            tmp->_left = pB;
        else
            tmp->_right = pB;
    }
​
    pA->_bf = pB->_bf = 0;
}

  2. RR 型：由于在 A 的右子树根节点的右子树上插入节点，A 的平衡因子由 -1 变成 -2，致使以 A 为根节点的子树失去平衡，则需进行一次向左的逆时针旋转操作。

    void RR(Node* pA)
{
    Node* pB = pA->_right;
    Node* pBL = pB->_left;
​
    pA->_right = pBL;
    if (pBL)
        pBL->_parent = pA;
​
    pB->_left = pA;
    Node* tmp = pA->_parent;
    pA->_parent = pB;
    pB->_parent = tmp;
​
    if (tmp == nullptr)  // 或者 _root == pA
    {
        _root = pB;
    }
    else
    {
        if (tmp->_left == pA)
            tmp->_left = pB;
        else
            tmp->_right = pB;
    }
​
    pA->_bf = pB->_bf = 0;
}

  3. LR 型：由于在 A 的左子树的根节点的右子树上插入节点，A 的平衡因子由 1 增至 2，致使以 A 为根节点的子树失去平衡，则需要进行两次旋转操作。

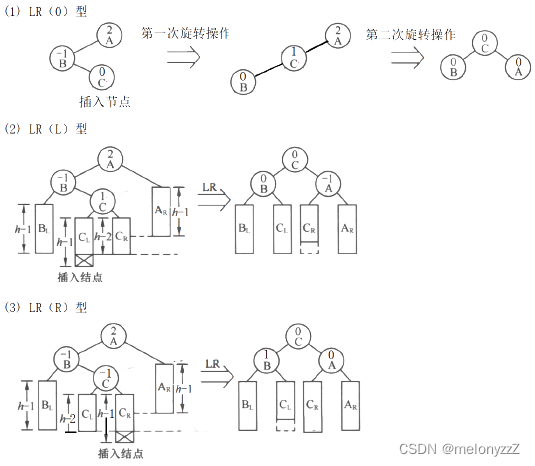
    void LR(Node* pA)
{
    Node* pB = pA->_left;
    Node* pC = pB->_right;
    int bf = pC->_bf;
​
    RR(pB);
    LL(pA);
​
    if (bf == 0)  // LR（0）型
    {
        pA->_bf = 0;
        pB->_bf = 0;
        pC->_bf = 0;
    }
    else if (bf == 1)  // LR（L）型
    {
        pA->_bf = -1;
        pB->_bf = 0;
        pC->_bf = 0;
    }
    else if (bf == -1)  // LR（R）型
    {
        pA->_bf = 0;
        pB->_bf = 1;
        pC->_bf = 0;
    }
}

  4. RL 型：由于在 A 的右子树根节点的左子树上插入节点，A 的平衡因子由 -1 变为 -2，致使以 A 为根节点的子树失去平衡，则旋转方法和 LR 型对称，也需进行两次旋转，先顺时针右旋，再逆时针左旋。

    void RL(Node* pA)
{
    Node* pB = pA->_right;
    Node* pC = pB->_left;
    int bf = pC->_bf;
​
    LL(pB);
    RR(pA);
​
    if (bf == 0)  // RL（0）型
    {
        pA->_bf = 0;
        pB->_bf = 0;
        pC->_bf = 0;
    }
    else if (bf == 1)  // RL（L）型
    {
        pA->_bf = 0;
        pB->_bf = -1;
        pC->_bf = 0;
    }
    else if (bf == -1)  // RL（R）型
    {
        pA->_bf = 1;
        pB->_bf = 0;
        pC->_bf = 0;
    }
}

总结：无论哪一种情况，在经过平衡旋转处理之后，以 B 或 C 为根的新子树为平衡二叉树，而且它们的高度和插入之前以 A 为根的子树相同。因此，当平衡的二叉搜索树因插入节点而失去平衡时，仅需对最小不平衡子树进行平衡旋转处理即可。

五、AVL 树的删除

AVL 树的删除算法与二叉搜索树类似，不同之处在于：若删除后破坏了 AVL 树的高度平衡性质，还需要做平衡化旋转。

  1. 如果被删节点 *cur 的左、右子树都不为空。首先找到左子树中键值最大的节点 *leftMax（或者找到右子树中键值最小的节点 *rightMin），然后进行交换，即 std::swap(cur->_kv, leftMax->_kv);， 此时被删节点就变成了 *leftMax，该节点的右子树一定为空。

  2. 如果被删节点 *cur 最多只有一个孩子 *child。可以把 *cur 的双亲节点 *parent 中原来指向 *cur 的指针改为指向 *child。如果 *cur 没有孩子，则 *parent 的相应指针置为 nullptr。由于以 *parent 为根节点的子树的高度缩短了 1，所以需沿着 *parent 通向根节点的路径，往上追踪高度的这一变化对路径上各个节点的影响。

考查 *cur 的祖先节点，若 *cur 在祖先节点的左子树中，则祖先节点的平衡因子 -1，反之，则祖先节点的平衡因子 +1。根据祖先节点更新后的平衡因子，按以下三种情况分别进行处理：

  1. 祖先节点的平衡因子原来为 0，在它的左子树或者右子树被缩短后，它的平衡因子变为 -1 或者 1。由于以该节点为根的子树的高度没有改变，则不需要往上更新了，删除结束。

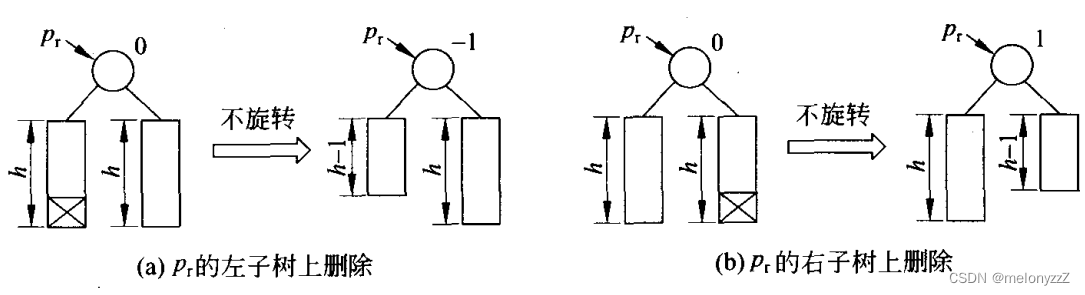
  2. 祖先节点的平衡因子原来为 1 或者 -1，在它的较高的子树被缩短后，它的平衡因子改为 0。此时以该节点为根的子树平衡，但其高度减 1，所以需要继续往上更新。

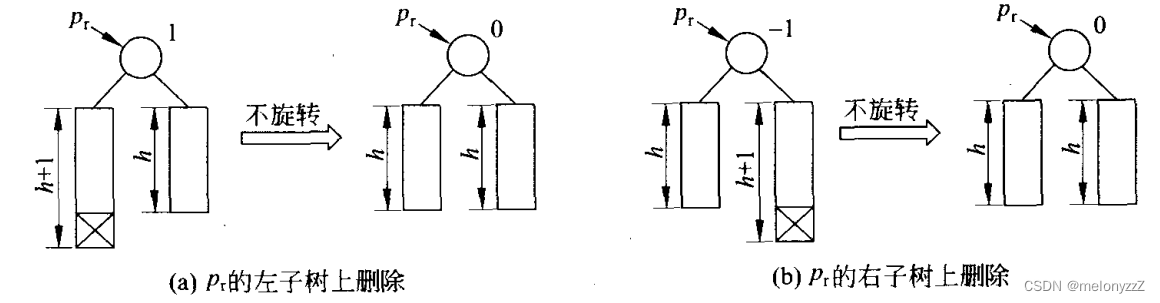
  3. 祖先节点的平衡因子原来为 -1 或者 1，在它的较矮的子树被缩短后，它的平衡因子变为 -2 或者 2。此时以该节点为根的子树不平衡，需要进行平衡化旋转来恢复平衡。

    根据祖先节点较高的子树的根（该子树未被缩短）的平衡因子，有如下 3 种平衡化操作：

    (1) 如果祖先节点较高的子树的根的平衡因子为 0，则执行一个单旋转来恢复子树的平衡。

    由于旋转平衡后以 *q 为根节点的子树的高度没有发生改变，所以不需要再往上更新了，删除结束。

    (2) 如果祖先节点较高的子树的根的平衡因子和祖先节点的平衡因子的正负号相同，则执行一个单旋转来恢复平衡。

    由于经过旋转平衡旋转后以 *q 为根节点的子树的高度降低了 1，所以需要继续往上更新。

    (3) 如果祖先节点较高的子树的根的平衡因子和祖先节点的平衡因子的正负号相反，则执行一个双旋转来恢复平衡。

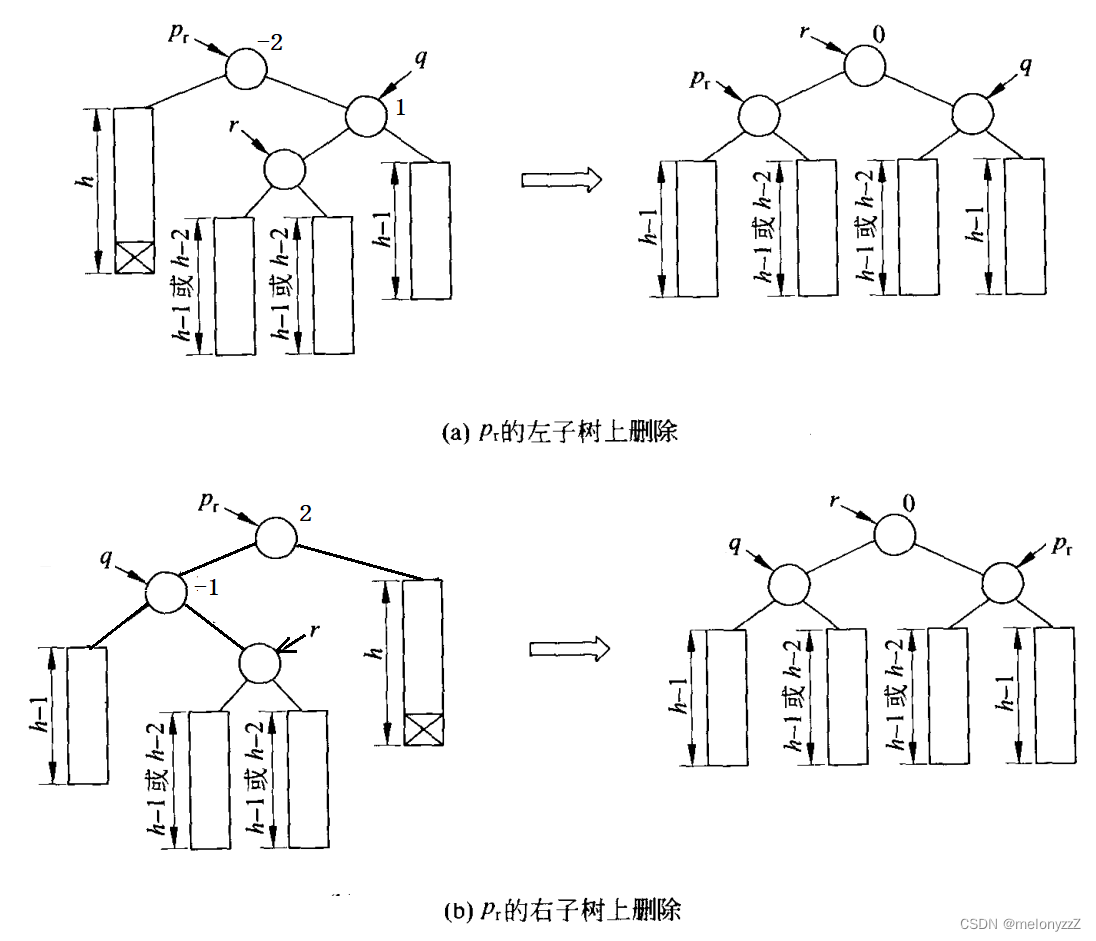
    由于经过平衡化处理后以 *r 为根的子树的高度降低了 1，所以还需要继续往上更新。

六、AVL 树的实现

6.1 - AVL.h

#pragma once
​
#include <utility>
​
template<class K, class V>
struct AVLNode
{
    AVLNode<K, V>* _left;
    AVLNode<K, V>* _right;
    AVLNode<K, V>* _parent;
    std::pair<K, V> _kv;
    int _bf;
​
    AVLNode(const std::pair<K, V>& kv = std::pair<K, V>())
        : _left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0)
    { } 
};
​
template<class K, class V>
class AVL
{
    typedef AVLNode<K, V> Node;
public:
    AVL() : _root(nullptr) { }
​
    ~AVL()
    {
        Destroy(_root);
    }
​
    bool isBalanced() const
    {
        return _isBalanced(_root);
    }
​
    bool insert(const std::pair<K, V>& kv)
    {
        if (_root == nullptr)
        {
            _root = new Node(kv);
            return true;
        }
​
        Node* parent = nullptr;
        Node* cur = _root;
        while (cur)
        {
            parent = cur;
            if (kv.first < cur->_kv.first)
                cur = cur->_left;
            else if (kv.first > cur->_kv.first)
                cur = cur->_right;
            else
                return false;
        }
​
        cur = new Node(kv);
        if (kv.first < parent->_kv.first)
            parent->_left = cur;
        else
            parent->_right = cur;
        cur->_parent = parent;  // 注意：这一步很容易被忽略
​
        // 往上更新 *cur 的祖先节点的平衡因子
        while (parent)
        {
            if (parent->_left == cur)
                ++parent->_bf;
            else
                --parent->_bf;
​
            if (parent->_bf == 0)
            {
                break;
            }
            else if (parent->_bf == 1 || parent->_bf == -1)
            {
                cur = parent;
                parent = parent->_parent;
            }
            else if (parent->_bf == 2 || parent->_bf == -2)
            {
                // 平衡二叉树的平衡调整
                if (parent->_bf == 2 && cur->_bf == 1)
                    LL(parent);
                else if (parent->_bf == -2 && cur->_bf == -1)
                    RR(parent);
                else if (parent->_bf == 2 && cur->_bf == -1)
                    LR(parent);
                else if (parent->_bf == -2 && cur->_bf == 1)
                    RL(parent);
                // 跳出循环
                break;
            }
        }
        return true;
    }
​
    bool erase(const std::pair<K, V>& kv)
    {
        Node* parent = nullptr;
        Node* cur = _root;
        while (cur)
        {
            if (kv.first == cur->_kv.first)
                break;
​
            parent = cur;
            if (kv.first < cur->_kv.first)
                cur = cur->_left;
            else
                cur = cur->_right;
        }
​
        if (cur == nullptr)  // 树为空或者在树中未找到被删节点
            return false;
​
        // 被删节点的左、右子树都不为空
        if (cur->_left && cur->_right)
        {
            parent = cur;
            Node* leftMax = cur->_left;
            while (leftMax->_right)
            {
                parent = leftMax;
                leftMax = leftMax->_right;
            }
            std::swap(cur->_kv, leftMax->_kv);
            cur = leftMax;  
            // 此时被删节点就变成了 *leftMax，该节点的右子树为空
        }
​
        // 被删节点最多只有一个孩子
        Node* child;
        if (cur->_left)
            child = cur->_left;
        else
            child = cur->_right;
​
        if (parent == nullptr)  // 被删节点为根节点
        {
            _root = child;  
        }
        else
        {
            if (parent->_left == cur)
            {
                --parent->_bf;
                parent->_left = child;
            }
            else
            {
                ++parent->_bf;
                parent->_right = child;
            }
​
            // 往上更新 *cur 的祖先节点的平衡因子
            bool isFirst = true;
            while (parent)
            {
                // 注意：在第一次循环中，child 可能为 nullptr，
                // 不能通过下面的方式判断 *cur 在其祖先节点的左子树中，还是右子树中，
                // 所以需要在循环外更新 *cur 的双亲节点的平衡因子，
                // 在循环内更新 *cur 其它祖先节点的平衡因子。
                if (isFirst == false)
                {
                    if (parent->_left == child)
                        --parent->_bf;
                    else
                        ++parent->_bf;
                }
                isFirst = false;
​
                if (parent->_bf == -1 || parent->_bf == 1)
                {
                    break;
                }
                else if (parent->_bf == -2 || parent->_bf == 2)
                {
                    int sign = 0;  // 祖先节点的平衡因子的正负号
                    Node* higher;
                    if (parent->_bf < 0)
                    {
                        sign = -1;
                        higher = parent->_right;
                    }
                    else
                    {
                        sign = 1;
                        higher = parent->_left;
                    }
​
                    if (higher->_bf == 0)
                    {
                        if (sign < 0)
                        {
                            RR(parent);
                            parent->_bf = -1;
                            higher->_bf = 1;
                        }
                        else
                        {
                            LL(parent);
                            parent->_bf = 1;
                            higher->_bf = -1;
                        }
                        break;  // 不需要继续往上更新，跳出循环
                    }
                    else if (higher->_bf == sign)  // 两节点的平衡因子同号
                    {
                        if (sign < 0)
                        {
                            RR(parent);
                            parent = higher;
                            child = parent->_left;
                        }
                        else
                        {
                            LL(parent);
                            parent = higher;
                            child = parent->_right;
                        }
                    }
                    else  // 两节点的平衡因子反号
                    {
                        if (sign < 0)
                        {
                            Node* tmp = parent->_right->_left;
                            RL(parent);
                            parent = tmp;
                            child = parent->_left;
                        }
                        else
                        {
                            Node* tmp = parent->_left->_right;
                            LR(parent);
                            parent = tmp;
                            child = parent->_right;
                        }
                    }
                }
                // 继续往上更新
                child = parent;
                parent = parent->_parent;
            }
        }
        delete cur;
        return true;
    }
private:
    void Destroy(Node*& root)
    {
        //【注意:root 为 _root 或者某个节点的左或右作指针的引用】
        if (root == nullptr)
            return;
​
        Destroy(root->_left);
        Destroy(root->_right);
        delete root;
        root = nullptr;
    }
​
    int Height(Node* root) const
    {
        if (root == nullptr)
            return 0;
​
        int leftHeight = Height(root->_left);
        int rightHeight = Height(root->_right);
        return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
    }
​
    bool _isBalanced(Node* root) const
    {
        if (root == nullptr)
            return true;
​
        int leftHeight = Height(root->_left);
        int rightHeight = Height(root->_right);
        return abs(leftHeight - rightHeight) < 2
            && _isBalanced(root->_left)
            && _isBalanced(root->_right);
    }
​
    void LL(Node* pA)
    {
        Node* pB = pA->_left;
        Node* pBR = pB->_right;
​
        pA->_left = pBR;
        if (pBR)
            pBR->_parent = pA;
​
        pB->_right = pA;
        Node* tmp = pA->_parent;
        pA->_parent = pB;
        pB->_parent = tmp;
​
        if (tmp == nullptr)  // 或者 pA == _root
        {
            _root = pB;
        }
        else
        {
            if (tmp->_left == pA)
                tmp->_left = pB;
            else
                tmp->_right = pB;
        }
​
        pA->_bf = pB->_bf = 0;
    }
​
    void RR(Node* pA)
    {
        Node* pB = pA->_right;
        Node* pBL = pB->_left;
​
        pA->_right = pBL;
        if (pBL)
            pBL->_parent = pA;
​
        pB->_left = pA;
        Node* tmp = pA->_parent;
        pA->_parent = pB;
        pB->_parent = tmp;
​
        if (tmp == nullptr)  // 或者 pA == _root
        {
            _root = pB;
        }
        else
        {
            if (tmp->_left == pA)
                tmp->_left = pB;
            else
                tmp->_right = pB;
        }
​
        pA->_bf = pB->_bf = 0;
    }
​
    void LR(Node* pA)
    {
        Node* pB = pA->_left;
        Node* pC = pB->_right;
        int bf = pC->_bf;
​
        RR(pB);
        LL(pA);
​
        if (bf == 0)  // LR（0）型
        {
            pA->_bf = 0;
            pB->_bf = 0;
            pC->_bf = 0;
        }
        else if (bf == 1)  // LR（L）型
        {
            pA->_bf = -1;
            pB->_bf = 0;
            pC->_bf = 0;
        }
        else if (bf == -1)  // LR（R）型
        {
            pA->_bf = 0;
            pB->_bf = 1;
            pC->_bf = 0;
        }
    }
​
    void RL(Node* pA)
    {
        Node* pB = pA->_right;
        Node* pC = pB->_left;
        int bf = pC->_bf;
​
        LL(pB);
        RR(pA);
​
        if (bf == 0)  // RL（0）型
        {
            pA->_bf = 0;
            pB->_bf = 0;
            pC->_bf = 0;
        }
        else if (bf == 1)  // RL（L）型
        {
            pA->_bf = 0;
            pB->_bf = -1;
            pC->_bf = 0;
        }
        else if (bf == -1)  // RL（R）型
        {
            pA->_bf = 1;
            pB->_bf = 0;
            pC->_bf = 0;
        }
    }
private:
    Node* _root;
};

6.2 - test.cpp

#include "AVL.h"
#include <iostream>
#include <vector>
#include <ctime>
using namespace std;
​
void TestAVL1()
{
    // int arr[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };  // ok
    int arr[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
    AVL<int, int> t;
    for (const auto& e : arr)
    {
        t.insert(make_pair(e, e));
        if (!t.isBalanced())
        {
            cout << "插入操作有误！" << endl;
            exit(-1);
        }
    }
    cout << "插入完成~" << endl;
​
    for (const auto& e : arr)
    {
        t.erase(make_pair(e, e));
        if (!t.isBalanced())
        {
            cout << "删除操作有误！" << endl;
            exit(-1);
        }
    }
    cout << "删除完成~" << endl;
}
​
void TestAVL2()
{
    srand((unsigned int)time(0));
    size_t N = 1000;
    vector<int> v;
    for (size_t i = 0; i < N; ++i)
    {
        v.push_back(rand());
    }
​
    AVL<int, int> t;
    for (const auto& e : v)
    {
        t.insert(make_pair(e, e));
        if (!t.isBalanced())
        {
            cout << "插入操作有误！" << endl;
            exit(-1);
        }
    }
    cout << "插入完成~" << endl;
​
    for (const auto& e : v)
    {
        t.erase(make_pair(e, e));
        if (!t.isBalanced())
        {
            cout << e << endl;
            cout << "删除操作有误！" << endl;
            exit(-1);
        }
    }
    cout << "删除完成~" << endl;
}
​
int main()
{
    TestAVL1();
    TestAVL2();
    return 0;
}

更多推荐

在Windos 10专业版搭建Fyne（Go 跨平台GUI）开发环境

目录在Windos10专业版搭建Fyne（Go跨平台GUI）开发环境一Fyne和MSYS2简介1.1Fyne1.2MSYS2二安装MSYS22.1下载MSYS22.2安装2.3环境变量设置2.4检测安装环境三参考文档在Windos10专业版搭建Fyne（Go跨平台GUI）开发环境一Fyne和MSYS2简介1.1Fyne

解密list的底层奥秘

🎈个人主页:🎈:✨✨✨初阶牛✨✨✨🐻强烈推荐优质专栏:🍔🍟🌯C++的世界(持续更新中)🐻推荐专栏1:🍔🍟🌯C语言初阶🐻推荐专栏2:🍔🍟🌯C语言进阶🔑个人信条:🌵知行合一金句分享:✨即使人生还有无数次失望的可能性,✨✨但我还是想活在理想主义的乌托邦里.✨目录一、list底层框架(1)节点类

使用Python进行供应链分析

供应链是生产和向客户交付货物所涉及的生产和物流网络。供应链分析是指分析供应链的各个组成部分，以了解如何提高供应链的有效性，为客户创造更多价值。所以，如果你想学习如何分析供应链，这篇文章是给你的。文章中，将带你完成使用Python进行供应链分析的任务。使用Python进行供应链分析导入必要的Python库和数据集开始供应

数据算法--7.2.2排序算法

一、希尔排序基本有序#include<stdio.h>voidInsertSort(intk[],intn){inti,j,temp;intgap=n;do{gap=gap/3+1;for(i=gap;i<n;i++){if(k[i]<k[i-gap]){temp=k[i];for(j=i-gap;k[j]>temp;

Mac/m1终端配置自动登录ssh服务器等后续操作

当我们每次连接ssh服务器的时候，都要输入账号密码等重复性的操作，这些动作让我们烦不胜烦。那怎么办呢？有没有什么玩意能让我们只输入一条命令，并且根据传参来自动的执行这些固定的操作呢？针对这个问题，我们就可以用expect神器来写一个自动化的交互脚本来解放我们的双手了。下面是实现流程：先定一个我们未来写脚本的文件夹mkd

一个线程运行时发生异常会怎样？

如果一个线程在运行时发生异常而没有被捕获（即未被适当的异常处理代码处理），则会导致以下几种情况之一：线程终止：线程会立即终止其执行，并将异常信息打印到标准错误输出（System.err）。这通常包括异常的类型、堆栈跟踪信息以及异常消息。ThreadDeath异常：在某些情况下，特定类型的未捕获异常ThreadDeath

package.json属性

添加链接描述一、必须属性name定义项目的名称，不能以".“和”_"开头，不能包含大写字母version定义项目的版本号，格式为：大版本号.次版本号.修订号二、描述信息description项目描述keywords项目关键词author项目作者contributors项目贡献者homepage项目主页地址reposit

如何用一行CSS实现10种现代布局

现代CSS布局使开发人员只需按几下键就可以编写十分有意义且强大的样式规则。上面的讨论和接下来的帖文研究了10种强大的CSS布局，它们实现了一些非凡的工作。超级居中：place-items:center对于第一个“单行”布局，让我们解决所有CSS领域中最大的谜团：居中。我想让您知道，使用place-items:cente

网络安全（黑客）自学

前言我是去年8月22日才正式学习网络安全的，因为在国营单位工作了4年，在广东一个月工资只有5000块，而且看不到任何晋升的希望，如果想要往上走，那背后就一定要有关系才行。而且国营单位的气氛是你干的多了，领导觉得你有野心，你干的不多，领导却觉得你这个人不错。我才24周岁，实在的受不了这种工作氛围，情绪已经压制了很多久，一

2023-09-21 LeetCode每日一题（收集树中金币）

2023-09-21每日一题一、题目编号2603.收集树中金币二、题目链接点击跳转到题目位置三、题目描述给你一个n个节点的无向无根树，节点编号从0到n-1。给你整数n和一个长度为n-1的二维整数数组edges，其中edges[i]=[ai,bi]表示树中节点ai和bi之间有一条边。再给你一个长度为n的数组coins，其

精品Python商铺摊位租赁管理系统

《[含文档+PPT+源码等]精品基于Python实现的商铺摊位管理系统设计与实现》该项目含有源码、文档、PPT、配套开发软件、软件安装教程、项目发布教程等软件开发环境及开发工具：开发语言：python使用框架：Django前端技术：JavaScript、VUE.js（2.X）、css3开发工具：pycharm、Visu

热文推荐
  1. xxl-job的原理（1）

    xxl-job的架构系统组成调度中心：进行任务统一调度，可以新增和管理执行器和任务；执行器：任务执行依赖的组件，一个执行器可以关联多个任务，添加的执行器可以自动注册到调度中心上；任务：具体的业务执行逻辑，针对该逻辑可以在调度中心配置定时策略，定时策略支持cron表达式和固定速率；系统架构![image-20230918

  2. 全国职业技能大赛云计算--高职组赛题卷⑤（容器云）

    全国职业技能大赛云计算--高职组赛题卷⑤（容器云）第二场次题目：容器云平台部署与运维任务2基于容器的web应用系统部署任务（15分）任务3基于容器的持续集成部署任务（15分）任务4Kubernetes容器云平台部署与运维（15分，本任务只公布考试范围，不公布赛题）需要环境的可以私信联系博主！！！第二场次题目：容器云平台

  3. android h5 共享停车系统myeclipse开发mysql数据库编程服务端java计算机程序设计

    一、源码特点javaandroidh5共享停车系统APP是一套完善的WEB+android设计系统，对理解JSPjava，安卓app编程开发语言有帮助（系统采用web服务端+APP端综合模式进行设计开发），系统具有完整的源代码和数据库，系统主要采用B/S模式开发。Android平台的共享停车系统1二、功能介绍具体实现如

  4. 「Java开发指南」在MyEclipse中的Spring开发（二）

    在上文中（点击这里回顾>>），我们主要介绍了一些Spring的基本概念、Spring项目配置及向导，本章节将继续介绍如何管理多个项目，Spring配置编辑器等，欢迎持续关注~MyEclipsev2023.1.2离线版下载(Q技术交流：742336981）4.管理多个Beans和项目除了使用bean配置文件编辑器来管理S

  5. 动态代理原理和设计模式详解

    一、什么是代理模式代理模式是一种设计模式，提供了对目标对象额外的访问方式，即可以通过代理访问目标对象，这样可以在不修改原目标对象的前提下，提供额外的方式进行访问，扩展目标对象的功能。通俗的说，例如你想租房，房子就是你的目标访问对象，那在中间的信息差巨大的情况下，你想要精准找到合适的房子，那么你可以找到中介，中介就是你的

  6. Selenium基础知识

    关于selenium你应该知道的selenium是什么？一个自动化测试的工具（系统测试）测试阶段：单元测试、集成测试、系统测试、验收测试自动化测试属于：系统测试自动测试工具：自动化功能测试工具和自动化性能测试selenium包括什么组件？seleniumide，selenium2(seleniumRC(服务)+webD

  7. 单例模式，适用于对象唯一的情景（设计模式与开发实践 P4）

    文章目录单例模式实现代理单例惰性单例上一章后续的内容是关于JS函数闭包的，考虑很多读者已经有了闭包基础或者希望通过实战理解，遂跳过上一章直接开始设计模式篇～需要注意的是，代码部分仅供参考，主要关注的内容是设计模式的思想和运用，结合到自己的实战中才是最好的单例模式单例模式的定义是：保证一个类只有一个实例，并提供一个访问他

  8. 什么是特权帐户和会话管理

    特权帐户和会话管理（PASM）是特权访问管理的一部分，它为用户提供通过远程会话对关键帐户和业务敏感型端点（如数据中心、数据库和应用程序）的管理访问权限。事实上，Gartner已将PASM列为PAM的关键支柱之一，与权限提升和委派管理以及安全远程访问并列。过度的特权伴随着过度的风险，员工拥有的管理权限越多，攻击面就越大。

  9. 中小企业建设数字化工厂，选择集成还是重构

    随着科技的飞速发展和市场竞争的日益激烈，数字化工厂管理系统已成为中小企业未来发展的必经之路。然而，对于许多中小企业来说，建设数字化工厂并非易事。在建设数字化工厂的过程中，企业需要面对许多问题，其中最关键的问题是：选择集成还是重构？首先，我们需要理解数字化工厂的内涵。数字化工厂是在数字化技术的基础上，将生产全过程数字化，